目录
目录
文章目录
  1. 概述
  2. RSA详解
  3. 双线性配对

信息安全之密码（专业总结）

2017.05.31 Shaowei_Teng 密码学  热度 ℃

概述

  • 总的来说，计算机系统及网络由于其本身的开放性和匿名性带来了信息安全的隐患。
  • 信息安全的5个基本要素：保密性、完整性、可控性、可用性、可审查性；而对于网络及网络交易而言，信息安全的基本需求是保密性、完整性、不可抵赖性。
  • 主要的安全的技术
    • 数据加密
    • 数据签名
    • 身份认证
    • 防火墙
    • 内容检查

  • 从TCP/IP五层网络结构看

    • 物理层：可以采用防窃听技术来加强通信线路的安全
    • 数据链路层：可以使用通信保密机技术来进行链路加密，使用L2TP、PPTP来实现二层隧道通信
    • 网络层：可以采用防火墙来处理信息内外网络边界的流动，利用IPSec建立透明的安全加密信道
    • 传输层：可以使用SSL对低层安全服务进行抽象和屏蔽
    • 应用层：最有效的一类做法是可以在传输层和应用层之间建立中间件层次，以实现通用的安全服务功能，通过定义统一的安全服务接口向应用层提供身份认证、访问控制、数据加密安全服务。

  • 数据加密技术与认证技术一起，构建起了安全的商业加密体系。传统的数据加密是保护数据的最基本方式，它只能防止第三者获得真实的数据（数据的保密性）；认证技术则可以解决否认、伪造、篡改和冒充的问题（数据的完整性和不可抵赖性）。

  • 数据加密技术

    • 对称密钥体制：加密系统的加密密钥和解密密钥相同，它的优点是具有很高的保密强度，但密钥的传输需要经过安全可靠地途径。
      • 分组密码、序列密码
      • DES、3DES、AES、IDEA
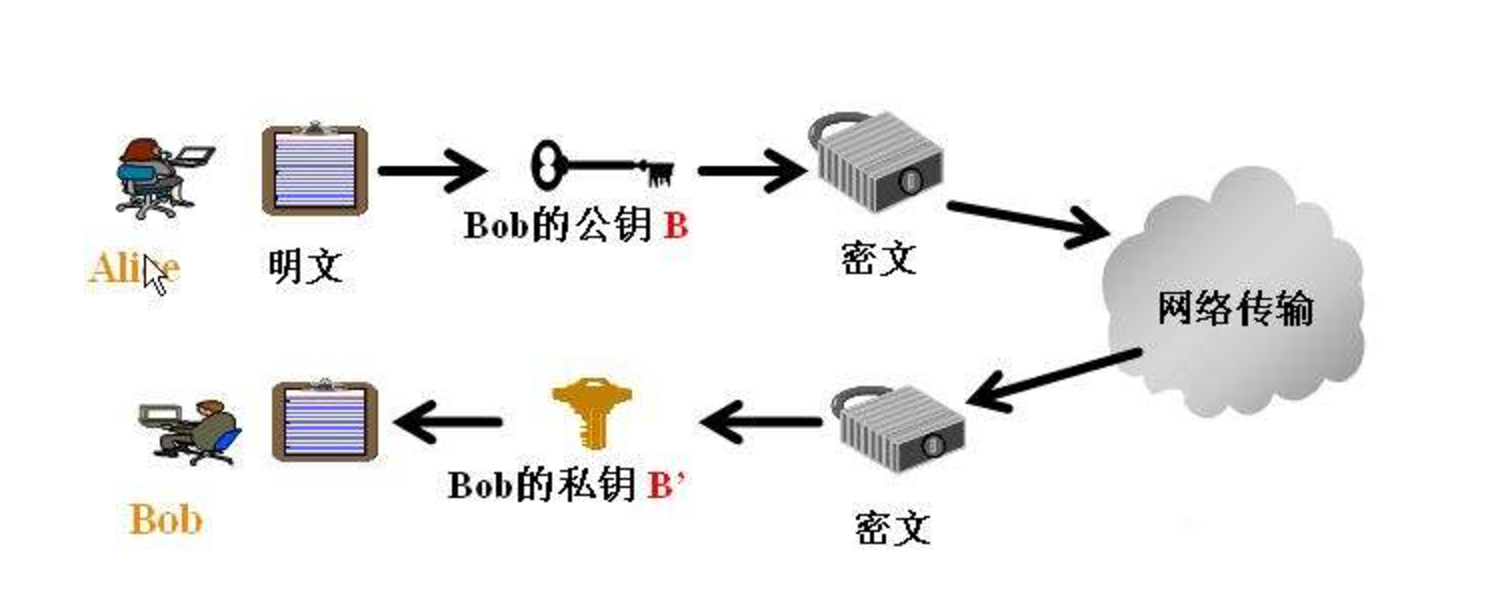
    • 非对称密钥体制（公钥密码体制）：加密系统的加密密钥和解密密钥不相同，它的优点在于适应开放性的使用环境，可以实现数字签名与验证。
      • Diffie-Hellman密钥交换算法:一种加密协议，允许双方在事先不了解对方的情况下，在不安全的通信信道中，共同建立共享密钥。该密钥以后可与一个对称密码一起，加密后续通讯。
      • RSA：它的理论基础是数论中的大数素分解难题，但如果使用RSA来加密大量的数据则速度太慢，因此RSA广范用于密钥的分发。
      • 现在主要有两类公钥算法
        • 大数素分解的困难
        • 以大数素为模来计算离散对数的困难
  • 认证技术
    • Hash函数和信息摘要（消息摘要）
      • 简单的说，hash函数就是把任意长的输入字符串变化成固定长的输出字符串的一种函数。输出字符串的长度称为hash函数的位数。
      • 常见的信息摘要算法
        • MD5（128位）
        • SHA-1（160位）
      • 目前应用最为广泛的是SHA-1和MD5，很多下载网站都提供下载文件的MD5码或SHA-1码校验，可以用来判别文件是否完整。
    • 数字签名技术

RSA详解

  • 公钥加密算法。首个适用于以签名作为加密的算法。RSA在电商行业中仍大规模使用，大家也相信它有足够安全长度的公钥。
  • RSA涉及到六个数字，p,q,n,φ(n),e,d。
    • p,q为素数
    • n = p*q
    • φ(n) = (p-1)(q-1)
    • 1 < e < φ(n)，且为素数
    • ed ≡ 1(modφ(n))，计算出d
    • 公钥（n，e），私钥（n，d）
  • 具体计算步骤
    • 假设 p = 3、q = 11（p，q都是素数即可。）
    • 则 n = p*q = 33；
    • φ(n) = (p-1)(q-1) = (3-1)(11-1) = 20；
    • e·d ≡ 1 (mod φ(n)),即 e·d = 20n+1 (n为正整数)；我们假设 n=1，则 e·d = 21。e、d为正整数，并且e与r互质，则 e = 3，d = 7。
    • 到这里，公钥和密钥已经确定。公钥为(n, e) = (33, 3)，密钥为(n, d) = (33, 7)。
  • 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class RSA {  
    /** 
     *  加密、解密算法 
     * @param (baseNum,key) 公钥或密钥 
     * @param message 数据 
     * @return 
     */  
    public static long rsa(int baseNum, int key, long message){  
        if(baseNum < 1 || key < 1){  
            return 0L;  
        }  
        //加密或者解密之后的数据  
        long rsaMessage = 0L;  
          
        //加密核心算法  
        rsaMessage = Math.round(Math.pow(message, key)) % baseNum;  
        return rsaMessage;  
    }  
    
    public static void main(String[] args){  
        //基数  
        int baseNum = 3 * 11;  
        //公钥  
        int keyE = 3;  
        //密钥  
        int keyD = 7;  
        //未加密的数据  
        long msg = 24L;  
        //加密后的数据  
        long encodeMsg = rsa(baseNum, keyE, msg);  
        //解密后的数据  
        long decodeMsg = rsa(baseNum, keyD, encodeMsg);  
    }
    
}

双线性配对

  • 双线性配对（Bilinear Pairing, 也叫双线性映射）最早在密码学中是扮演者负面的角色。2000年，Joux利用双线性配对构造了一个三方密钥交换协议。随后在2001年，Boneh和Franklin利用它构造了第一个实用并且可证安全的基于身份的加密方案（Identity-Based Encryption， IBE）。从此开始，双线性配对才在密码学中得到了广泛的应用。

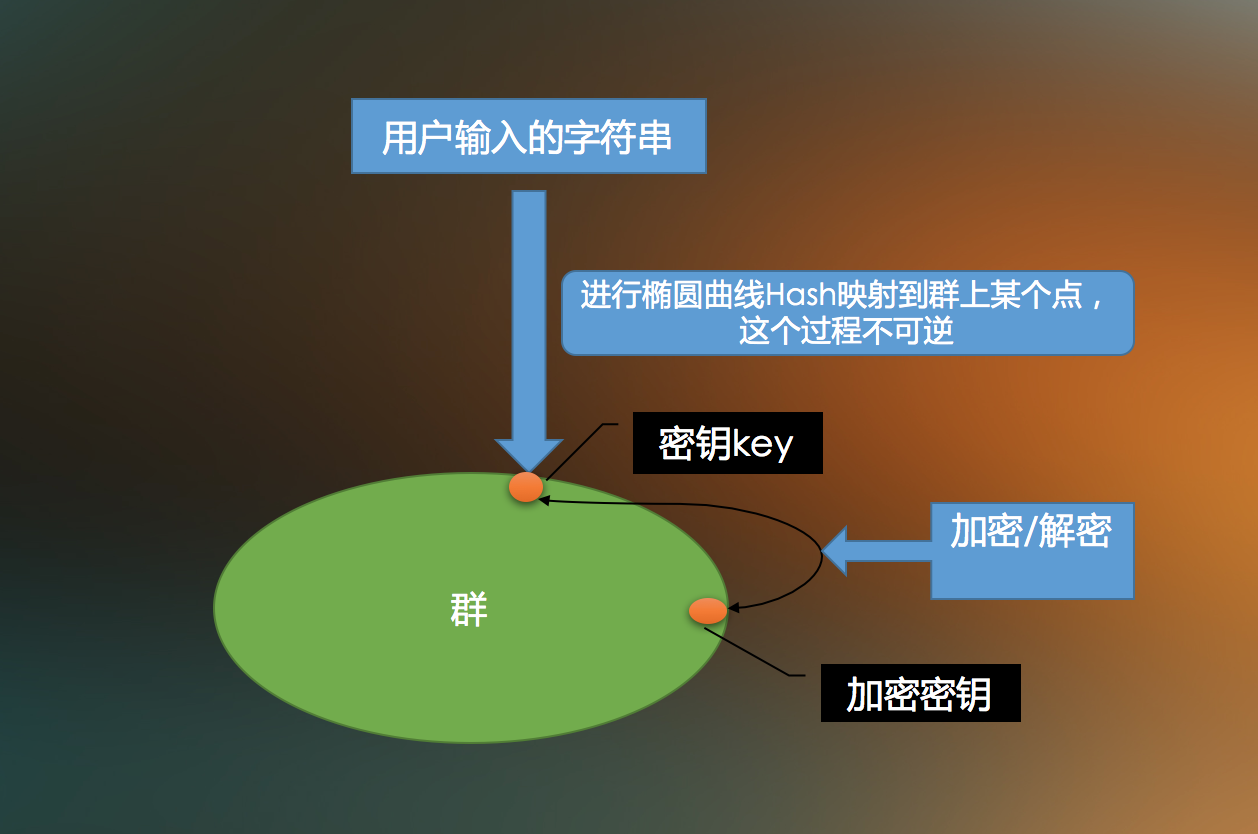
  • 现在使用双线性对实现的加密方案，实际上都是密钥封装方案，也就是封装一个随机的群上的密钥，然后调用单钥体制对消息进行加密或者解密操作。

  • 当前的双线性配对是基于群的，那么下面先讲解群的相关概念。

  • 什么是群？

    • 群本身就是某个数学对象（集合）所有的自同构构成的集合。
    • 自同构：对于一个集合A，A中定义一个闭合运算○，存在一个A与A之间的映射φ ，若φ为一双射，且对于A内任意元素a,b都有φ（a○b）=φ（a）○φ（b）则这个映射φ 叫做一个对于○ 来说的A的自同构。

  • 离散对数群

    • 在离散对数群中有一个难题，成为了离散对数难题。给定群的生成元g，和某一个群中的元素g^x，求解x本身很困难。有的人要问了，这个挺简单的啊，求log不就行了吗？需要注意的是，在连续域上面，确实有求log的快速算法（比如用数学分析中的Taylor展示求法，或者各种数值分析中的逼近算法等等），但是这些算法都是逼近算法，并不能求出准确解。当然了，一般数的log结果也是一个无线不循环小数，只能用逼近算法求。但是，在离散对数群中，我们是在用整数和整数做解，根本没有逼近算法这么回事…有兴趣的同学，可以了解一下离散对数群，并且设置一个生成元g，来尝试求一求一个数的离散对数，就会发现只能用枚举的算法来求。
    • 但是，在密码学中，这个计算困难假设不太好用，因此密码学家扩充了离散对数难题，提出了很多别的困难假设，以用于安全性证明。其中，最直接也是最简单的扩展，为计算Diffie-Hellman问题（Computataional Diffie-Hellman Problem，CDH），以及确定Diffie-Hellman问题（Decision Diffie-Hellman Problem，DDH）。
    • CDH问题是说，给定生成元g，两个群中的元素g^x，g^y，再不给定x，y的情况下，求g^{xy}。DDH问题是：同样给定生成元g，两个群中的元素g^x，g^y，再给定群的一个元素g^z，确定是否满足g^z = g^{xy}。CDH问题和DDH问题是很多加密方案和签名方案的安全基础，如著名的El Gamal加密方案。

  • 如图